Taller de regresión lineal

En los siguientes problemas vamos a utilizar unas bases de datos simuladas, donde en cada base ocurre algo especial que debemos intentar visualizar y modelar de forma convenienteusando regresión lineal múltiple. En todos los casos suponemos que tenemos una base de datos de niños, donde se ha recogido el sexo con una variable que indica con el valor 1 a las mujeres (0 para los Hombres), Edad y Talla. Nuestra intención es ver como el sexo y la edad explican la talla.

Ejemplo 1

Descargue la base de datos regresion-030-1.sav y exploramos las primeras líneas:

df=read_sav("datos/regresion-030-1.sav", user_na=FALSE) %>% haven::as_factor() %>% 
  mutate(Sexo=Mujer) %>% select(Sexo,Edad,Talla)

df %>% head()  %>% knitr::kable(booktabs=T)

Sexo	Edad	Talla
Mujer	7.5	142
Mujer	8.3	123
Hombre	5.8	121
Mujer	5.6	127
Hombre	6.7	122
Mujer	7.1	129

Antes de comenzar a analizar los datos hacemos una representación gráfica del contenido de la base de datos:

ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()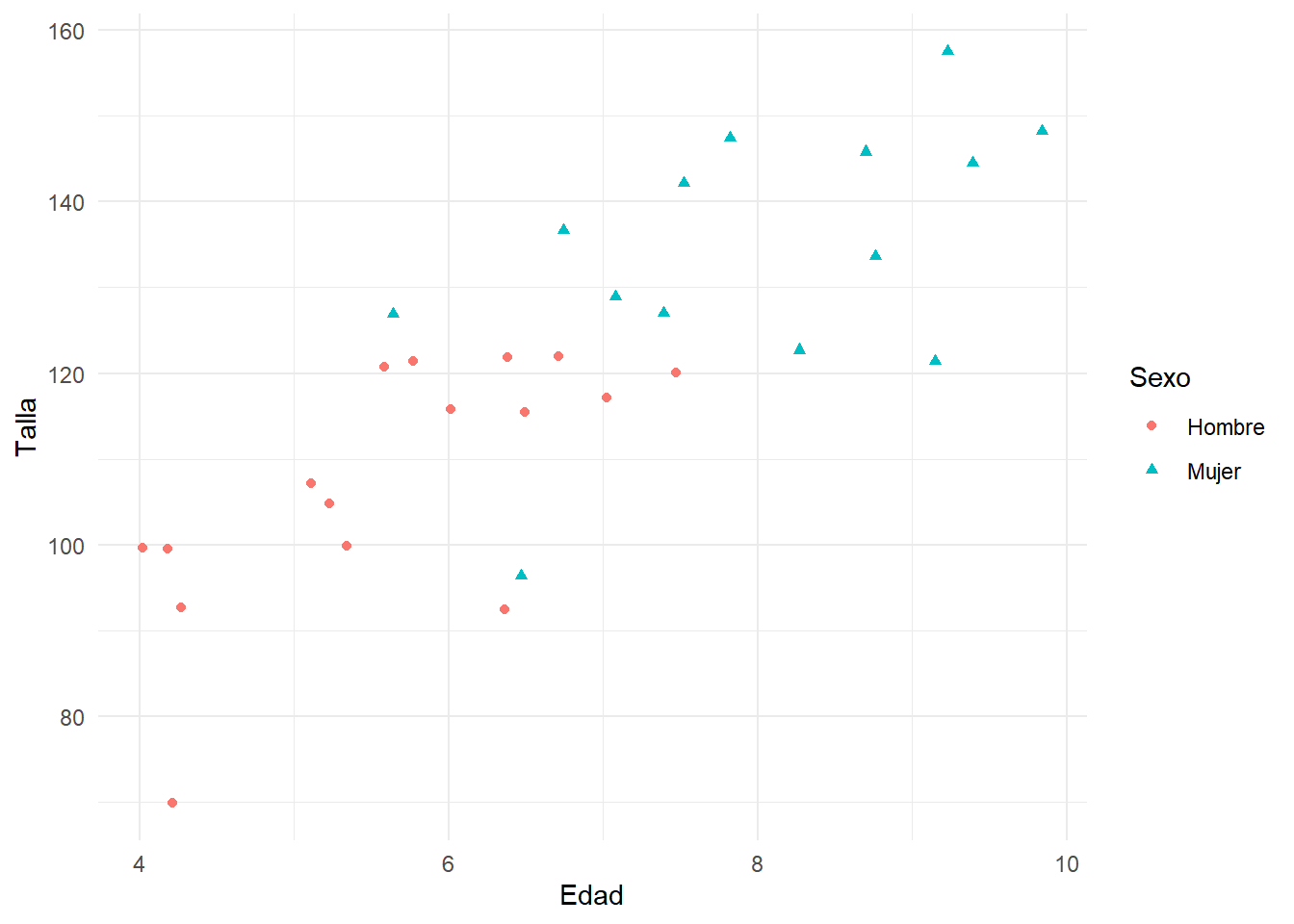

A simple vista, los individuos parecen tener mas talla con la edad sin importar el sexo, aunque por otro lado se observa que los varones son más jóvenes y pequeños, y las mujeres son de más edad y altas. Tenemos que hay confusión entre el sexo y la edad para explicar la talla. Si estudiamos de forma simple como el sexo explica la talla, tendríamos que las mujeres, sin tener en cuenta otra cosa son más altas que los hombres:

ggplot(df, aes(x=Sexo, y=Talla))+geom_boxplot()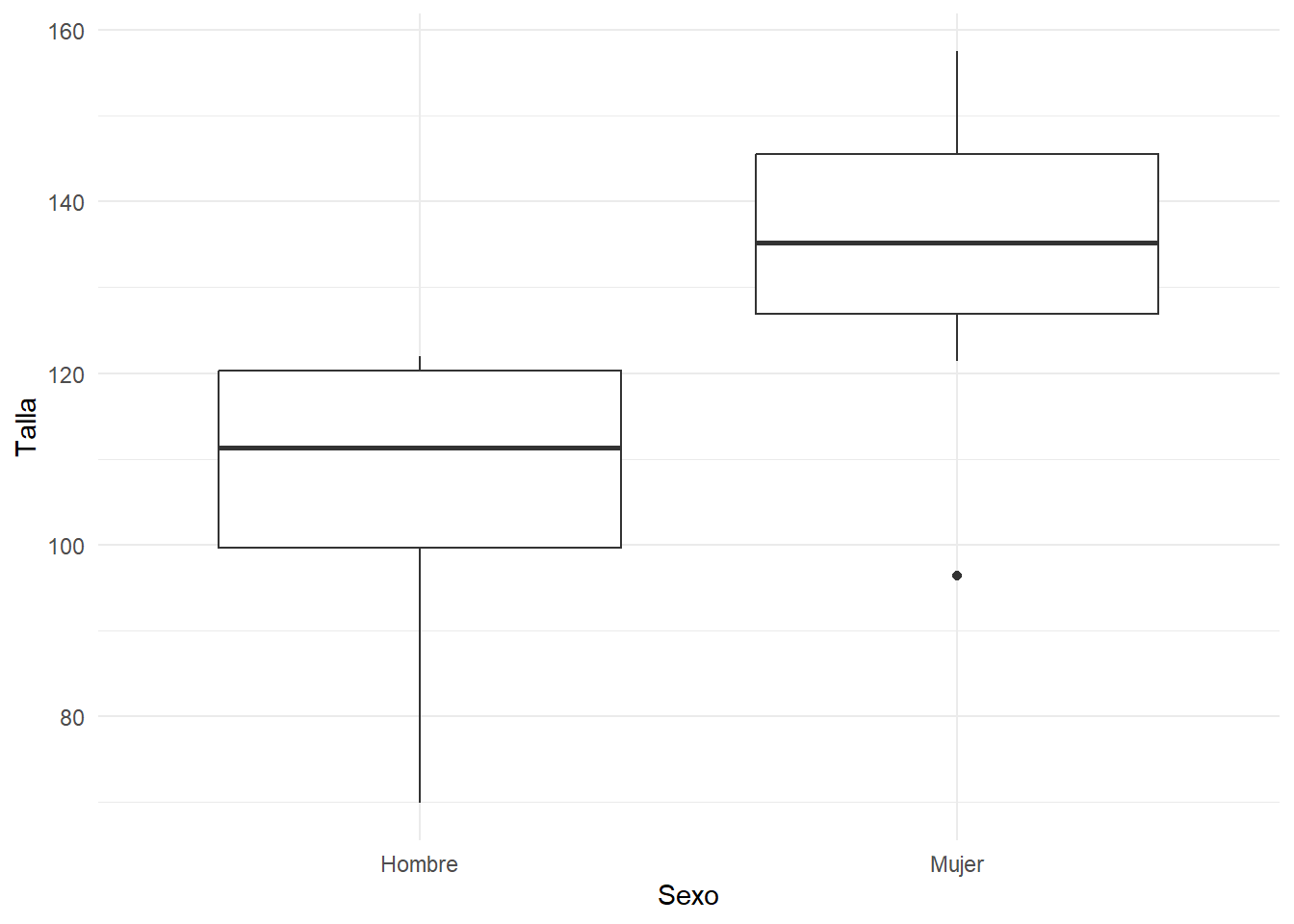

La causa de este resultado es no haber tenido en cuenta el ajuste por Edad en el analisis. ¿Cuál de los siguientes modelos le parece más interesante para describir la Altura de los niños?

dfAumentado <- broom::augment(lm(Talla ~ Edad+Sexo,data=df))
plot_SoloSexo=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE,formula = y ~ 1)+ggtitle("(1) Talla ~ Sexo")+ guides(color=FALSE,shape=FALSE)
plot_SoloEdad=ggplot(df, aes(x=Edad,y=Talla))+geom_point(aes(shape=Sexo,color=Sexo))+
  geom_smooth(method = "lm",se=FALSE)+ggtitle("(2) Talla ~ Edad")+ guides(color=FALSE,shape=FALSE)
plot_SexoEdad=ggplot(dfAumentado, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_line(aes(y = .fitted))+ggtitle("(3) Talla ~ Sexo+Edad")+ guides(color=FALSE,shape=FALSE)
plot_Interaccion=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE) +ggtitle("(4) Talla ~ Sexo+Edad+ Sexo:Edad")+ guides(color=FALSE,shape=FALSE)
grid.arrange(plot_SoloSexo,plot_SoloEdad,plot_SexoEdad,plot_Interaccion)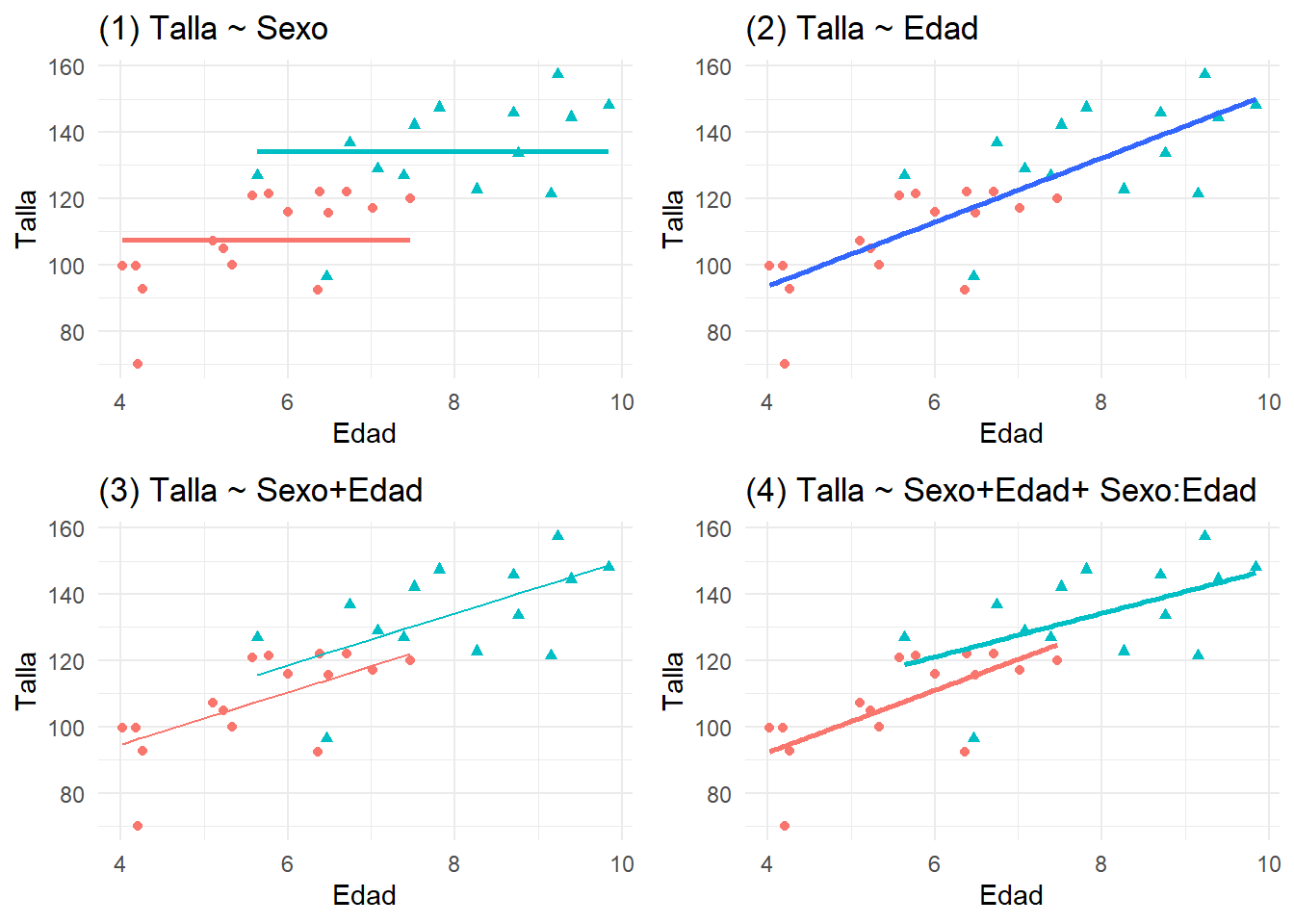

Los cuatro modelos de regresión respectivos son:

Modelo 1: La talla sólo depende del sexo.
Modelo 2: La talla sólo depende de la altura (mi favorito, por su simplicidad).
Modelo 3 La talla depende de la altura, y hay un pequeño efecto debido al sexo. las dos líneas son paralelas, siendo la distancia vertical entre ambas el efecto estimado atribuible al sexo.
Modelo 4 La talla depende de la altura para cada sexo, con rectas que no tienen por qué ser paralelas. Se ajusta la recta dentro de cada grupo. Esto es equivalente a considerar que hay un término de interacción que permite que cada recta tenga pendientes diferentes. Este modelo parece demasiado complicado.

El análisis de estos modelos lo encontramos en la siguiente tabla:

modeloSexo <- df %>% lm(Talla ~ Sexo, data=.)
modeloEdad <- df %>% lm(Talla ~ Edad, data=.)
modeloSexoEdad <- df %>% lm(Talla ~ Sexo+Edad, data=.)
modeloInteraccion <- df %>% lm(Talla ~ Sexo*Edad, data=.)
tab_model(modeloSexo, modeloEdad,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	107.55	3.75	<0.001	54.88	9.49	<0.001
Sexo: Mujer	26.68	5.49	<0.001
Edad				9.66	1.37	<0.001
Observations	30			30
R² / R² adjusted	0.458 / 0.438			0.640 / 0.627
AIC	251.555			239.247

tab_model(modeloSexoEdad,modeloInteraccion,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	63.15	11.49	<0.001	54.73	16.70	0.003
Sexo: Mujer	8.04	6.42	0.222	26.80	27.58	0.340
Edad	7.88	1.97	<0.001	9.37	2.91	0.003
SexoMujer:Edad				-2.79	3.98	0.490
Observations	30			30
R² / R² adjusted	0.660 / 0.635			0.666 / 0.628
AIC	239.556			240.996

El primer modelo, es el menos adecuado. Es el de menor \(R^2\), y atribuye un efecto significativo poramente al sexo, cuando en todos los demás modelos en que se incluye la edad, el sexo no tiene efecto significativo. Lo que vemos es debido al efecto confusor de la edad, que no ha sido tenido en cuenta.

El segundo modelo es el que tomaría como más adecuado por su parsimonia. Es simple y parece una buena simplificación de las observaciones. La bondad de ajuste \(R^2\) es prácticamente tan buena como se puede conseguir, y tiene el menor AIC. La única variable de la que depende (edad) el modelo tiene un efecto estadísticamente significativo.

El tercer modelo posee el mayor \(R2\) ajustado. Nos indica que la edad tiene efecto significativo en la talla, y que el sexo no tiene efecto significativo en la talla. Si queremos estudiar qué efecto tiene la edad en la talla, descontando/ajustando/teniendo en cuenta el sexo, es el modelo a utilizar.

El cuarto modelo es demasiado complicado. Atendiendo al criterio de \(R^2\), parece el mejor, pero eso es lógico ya que contiene a todas las variables explicativas y además su interacción. La reducción de \(R^2\) ajustado con respecto al tercer modelo, así como el aumento en AIC, y la falta de significación del término de interacción de Sexo con Edad, nos invitan a abandonarlo. En caso de querer un modelo complejo, el tercero es lo suficientemente complejo.

Ejemplo 2

Descargue la base de datos regresion-200-1.sav, que contiene datos similares al anterior, pero ahora la muestra está formada por 200 individuos. ¿No cree que el segundo modelo es el más adecuado?

df=read_sav("datos/regresion-200-1.sav", user_na=FALSE) %>% haven::as_factor() %>% 
  mutate(Sexo=Mujer) %>% select(Sexo,Edad,Talla)

dfAumentado <- broom::augment(lm(Talla ~ Edad+Sexo,data=df))
plot_SoloSexo=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE,formula = y ~ 1)+ggtitle("(1) Talla ~ Sexo")+ guides(color=FALSE,shape=FALSE)
plot_SoloEdad=ggplot(df, aes(x=Edad,y=Talla))+geom_point(aes(shape=Sexo,color=Sexo))+
  geom_smooth(method = "lm",se=FALSE)+ggtitle("(2) Talla ~ Edad")+ guides(color=FALSE,shape=FALSE)
plot_SexoEdad=ggplot(dfAumentado, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_line(aes(y = .fitted))+ggtitle("(3) Talla ~ Sexo+Edad")+ guides(color=FALSE,shape=FALSE)
plot_Interaccion=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE) +ggtitle("(4) Talla ~ Sexo+Edad+ Sexo:Edad")+ guides(color=FALSE,shape=FALSE)
grid.arrange(plot_SoloSexo,plot_SoloEdad,plot_SexoEdad,plot_Interaccion)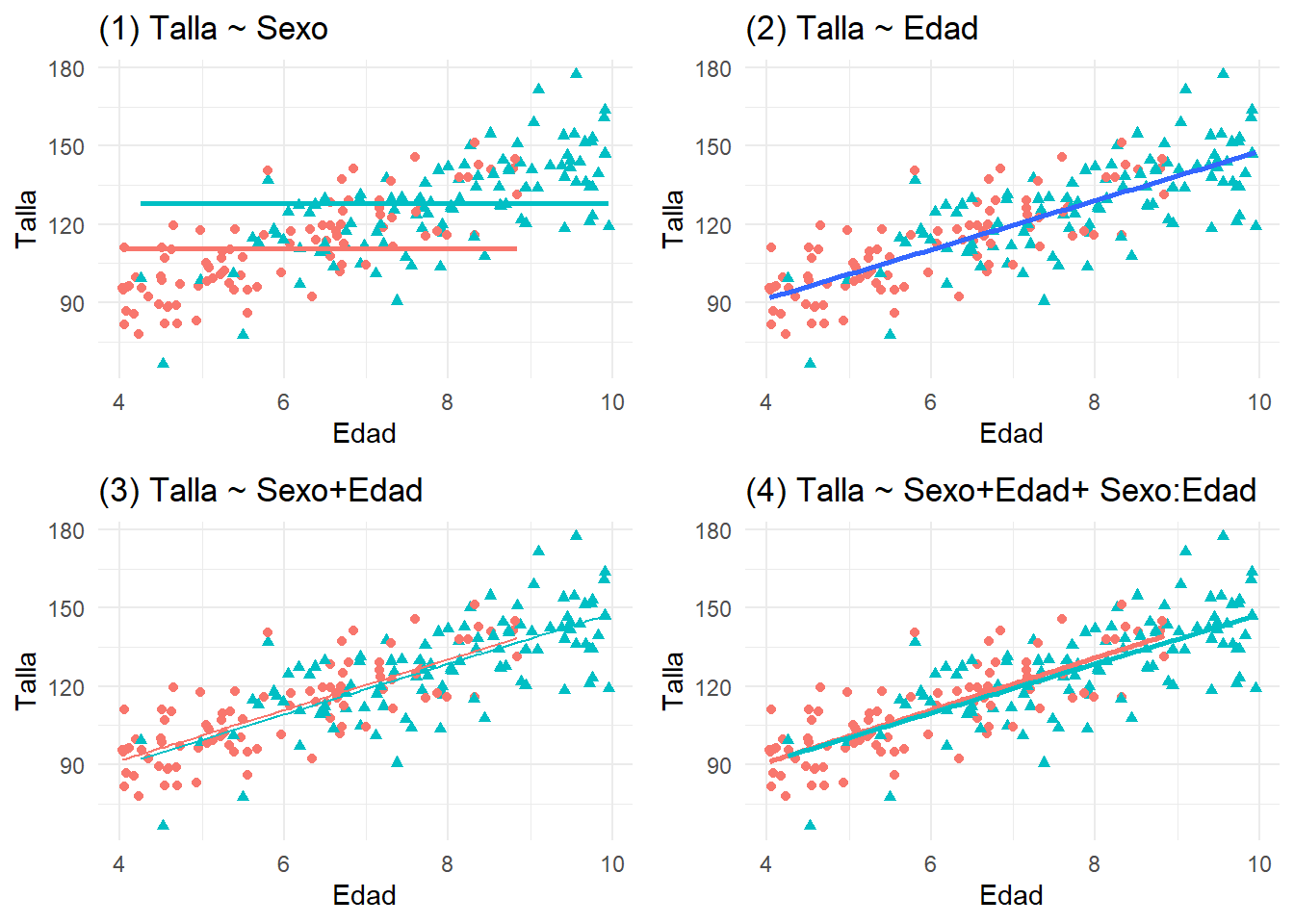

modeloSexo <- df %>% lm(Talla ~ Sexo, data=.)
modeloEdad <- df %>% lm(Talla ~ Edad, data=.)
modeloSexoEdad <- df %>% lm(Talla ~ Sexo+Edad, data=.)
modeloInteraccion <- df %>% lm(Talla ~ Sexo*Edad, data=.)
tab_model(modeloSexo, modeloEdad,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	110.52	1.88	<0.001	53.76	3.63	<0.001
Sexo: Mujer	17.56	2.56	<0.001
Edad				9.41	0.50	<0.001
Observations	200			200
R² / R² adjusted	0.192 / 0.188			0.640 / 0.638
AIC	1728.169			1566.659

tab_model(modeloSexoEdad,modeloInteraccion,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	52.66	3.90	<0.001	50.74	5.62	<0.001
Sexo: Mujer	-1.66	2.10	0.431	2.40	8.80	0.785
Edad	9.70	0.62	<0.001	10.02	0.92	<0.001
SexoMujer:Edad				-0.59	1.24	0.635
Observations	200			200
R² / R² adjusted	0.641 / 0.637			0.641 / 0.636
AIC	1568.027			1569.797

Ejemplo 3

Descargue la base de datos regresion-030-2.sav. En este caso tenemos niños que a igualdad de edad suelen ser más altos que las niñas. En ambos sexos, se crece con la edad a un ritmo similar. ¿Qué modelo cree que es más adecuado utilizar?

df=read_sav("datos/regresion-030-2.sav", user_na=FALSE) %>% haven::as_factor() %>% 
  mutate(Sexo=Mujer) %>% select(Sexo,Edad,Talla)

dfAumentado <- broom::augment(lm(Talla ~ Edad+Sexo,data=df))
plot_SoloSexo=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE,formula = y ~ 1)+ggtitle("(1) Talla ~ Sexo")+ guides(color=FALSE,shape=FALSE)
plot_SoloEdad=ggplot(df, aes(x=Edad,y=Talla))+geom_point(aes(shape=Sexo,color=Sexo))+
  geom_smooth(method = "lm",se=FALSE)+ggtitle("(2) Talla ~ Edad")+ guides(color=FALSE,shape=FALSE)
plot_SexoEdad=ggplot(dfAumentado, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_line(aes(y = .fitted))+ggtitle("(3) Talla ~ Sexo+Edad")+ guides(color=FALSE,shape=FALSE)
plot_Interaccion=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE) +ggtitle("(4) Talla ~ Sexo+Edad+ Sexo:Edad")+ guides(color=FALSE,shape=FALSE)
grid.arrange(plot_SoloSexo,plot_SoloEdad,plot_SexoEdad,plot_Interaccion)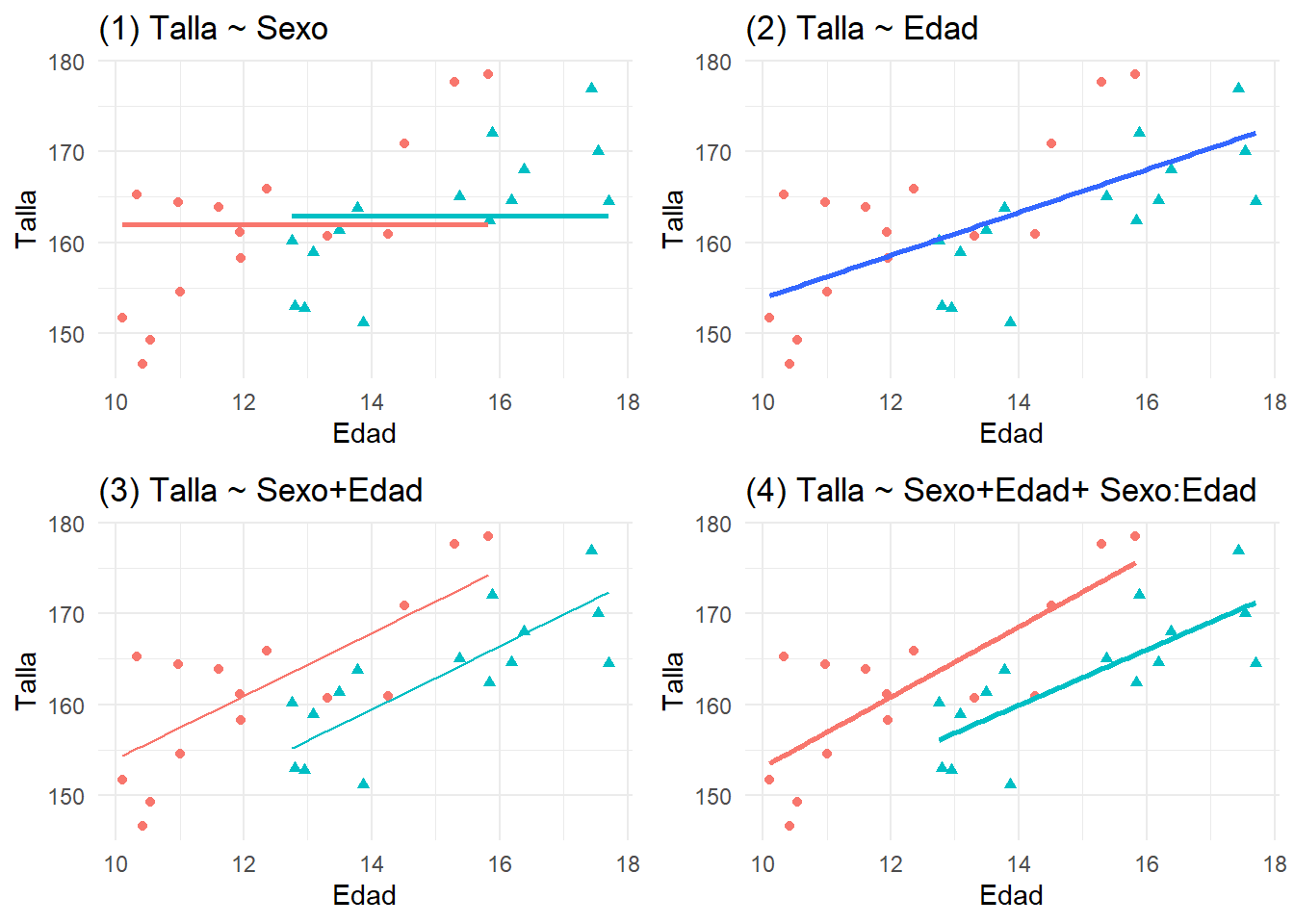

modeloSexo <- df %>% lm(Talla ~ Sexo, data=.)
modeloEdad <- df %>% lm(Talla ~ Edad, data=.)
modeloSexoEdad <- df %>% lm(Talla ~ Sexo+Edad, data=.)
modeloInteraccion <- df %>% lm(Talla ~ Sexo*Edad, data=.)
tab_model(modeloSexo, modeloEdad,show.se = TRUE,show.ci = FALSE,show.aic = TRUE)%>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	161.98	2.15	<0.001	130.31	6.99	<0.001
Sexo: Mujer	0.99	3.04	0.746
Edad				2.36	0.51	<0.001
Observations	30			30
R² / R² adjusted	0.004 / -0.032			0.437 / 0.417
AIC	216.149			199.024

tab_model(modeloSexoEdad,modeloInteraccion,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	119.32	6.71	<0.001	114.55	9.31	<0.001
Sexo: Mujer	-8.39	2.41	0.002	2.63	14.96	0.862
Edad	3.47	0.53	<0.001	3.86	0.75	<0.001
SexoMujer:Edad				-0.80	1.08	0.462
Observations	30			30
R² / R² adjusted	0.611 / 0.582			0.619 / 0.575
AIC	189.919			191.283

Ejemplo 4

Descargue la base de datos regresion-200-2.sav. Es como el anterior, pero con una muestra mucho mayor. Observe como con el aumento del tamaño de muestra se reducen los errores estándar/típicos de estimación de los parámetros, lo que puede ofrecer unos p más pequeños eventualmente, pero nada más cambia notablemente.

df=read_sav("datos/regresion-200-2.sav", user_na=FALSE) %>% haven::as_factor() %>% 
  mutate(Sexo=Mujer) %>% select(Sexo,Edad,Talla)

dfAumentado <- broom::augment(lm(Talla ~ Edad+Sexo,data=df))
plot_SoloSexo=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE,formula = y ~ 1)+ggtitle("(1) Talla ~ Sexo")+ guides(color=FALSE,shape=FALSE)
plot_SoloEdad=ggplot(df, aes(x=Edad,y=Talla))+geom_point(aes(shape=Sexo,color=Sexo))+
  geom_smooth(method = "lm",se=FALSE)+ggtitle("(2) Talla ~ Edad")+ guides(color=FALSE,shape=FALSE)
plot_SexoEdad=ggplot(dfAumentado, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_line(aes(y = .fitted))+ggtitle("(3) Talla ~ Sexo+Edad")+ guides(color=FALSE,shape=FALSE)
plot_Interaccion=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE) +ggtitle("(4) Talla ~ Sexo+Edad+ Sexo:Edad")+ guides(color=FALSE,shape=FALSE)
grid.arrange(plot_SoloSexo,plot_SoloEdad,plot_SexoEdad,plot_Interaccion)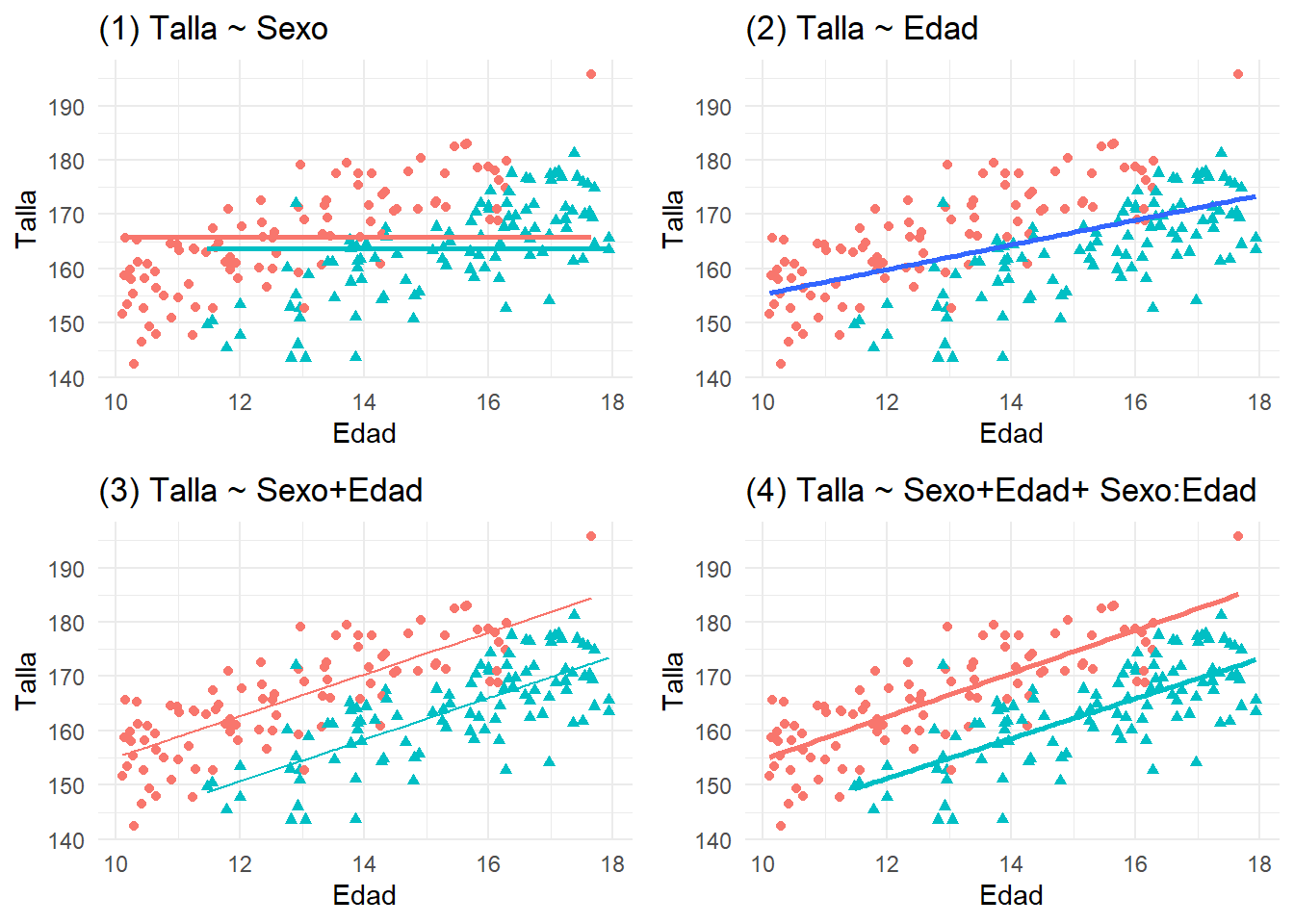

modeloSexo <- df %>% lm(Talla ~ Sexo, data=.)
modeloEdad <- df %>% lm(Talla ~ Edad, data=.)
modeloSexoEdad <- df %>% lm(Talla ~ Sexo+Edad, data=.)
modeloInteraccion <- df %>% lm(Talla ~ Sexo*Edad, data=.)
tab_model(modeloSexo, modeloEdad,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	165.89	0.94	<0.001	132.61	3.50	<0.001
Sexo: Mujer	-2.10	1.30	0.109
Edad				2.27	0.24	<0.001
Observations	200			200
R² / R² adjusted	0.013 / 0.008			0.304 / 0.301
AIC	1459.562			1389.670

tab_model(modeloSexoEdad,modeloInteraccion,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	116.80	3.03	<0.001	115.06	4.06	<0.001
Sexo: Mujer	-12.04	1.04	<0.001	-7.76	6.72	0.249
Edad	3.83	0.23	<0.001	3.97	0.31	<0.001
SexoMujer:Edad				-0.30	0.47	0.520
Observations	200			200
R² / R² adjusted	0.587 / 0.582			0.587 / 0.581
AIC	1287.533			1289.111

Ejemplo 5

Descargue la base de datos regresion-020-3.sav. En este caso tenemos niños y niñas que hacia los 10 años tienen la misma talla, pero de ahí en adelante, los niños crecen a un ritmo mayor que las niñas (aunque es dificil apreciar dicho efecto con muestras pequeñas) ¿Qué modelo cree que lo refleja mejor?

df=read_sav("datos/regresion-020-3.sav", user_na=FALSE) %>% haven::as_factor() %>% 
  mutate(Sexo=Mujer) %>% select(Sexo,Edad,Talla)

dfAumentado <- broom::augment(lm(Talla ~ Edad+Sexo,data=df))
plot_SoloSexo=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE,formula = y ~ 1)+ggtitle("(1) Talla ~ Sexo")+ guides(color=FALSE,shape=FALSE)
plot_SoloEdad=ggplot(df, aes(x=Edad,y=Talla))+geom_point(aes(shape=Sexo,color=Sexo))+
  geom_smooth(method = "lm",se=FALSE)+ggtitle("(2) Talla ~ Edad")+ guides(color=FALSE,shape=FALSE)
plot_SexoEdad=ggplot(dfAumentado, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_line(aes(y = .fitted))+ggtitle("(3) Talla ~ Sexo+Edad")+ guides(color=FALSE,shape=FALSE)
plot_Interaccion=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE) +ggtitle("(4) Talla ~ Sexo+Edad+ Sexo:Edad")+ guides(color=FALSE,shape=FALSE)
grid.arrange(plot_SoloSexo,plot_SoloEdad,plot_SexoEdad,plot_Interaccion)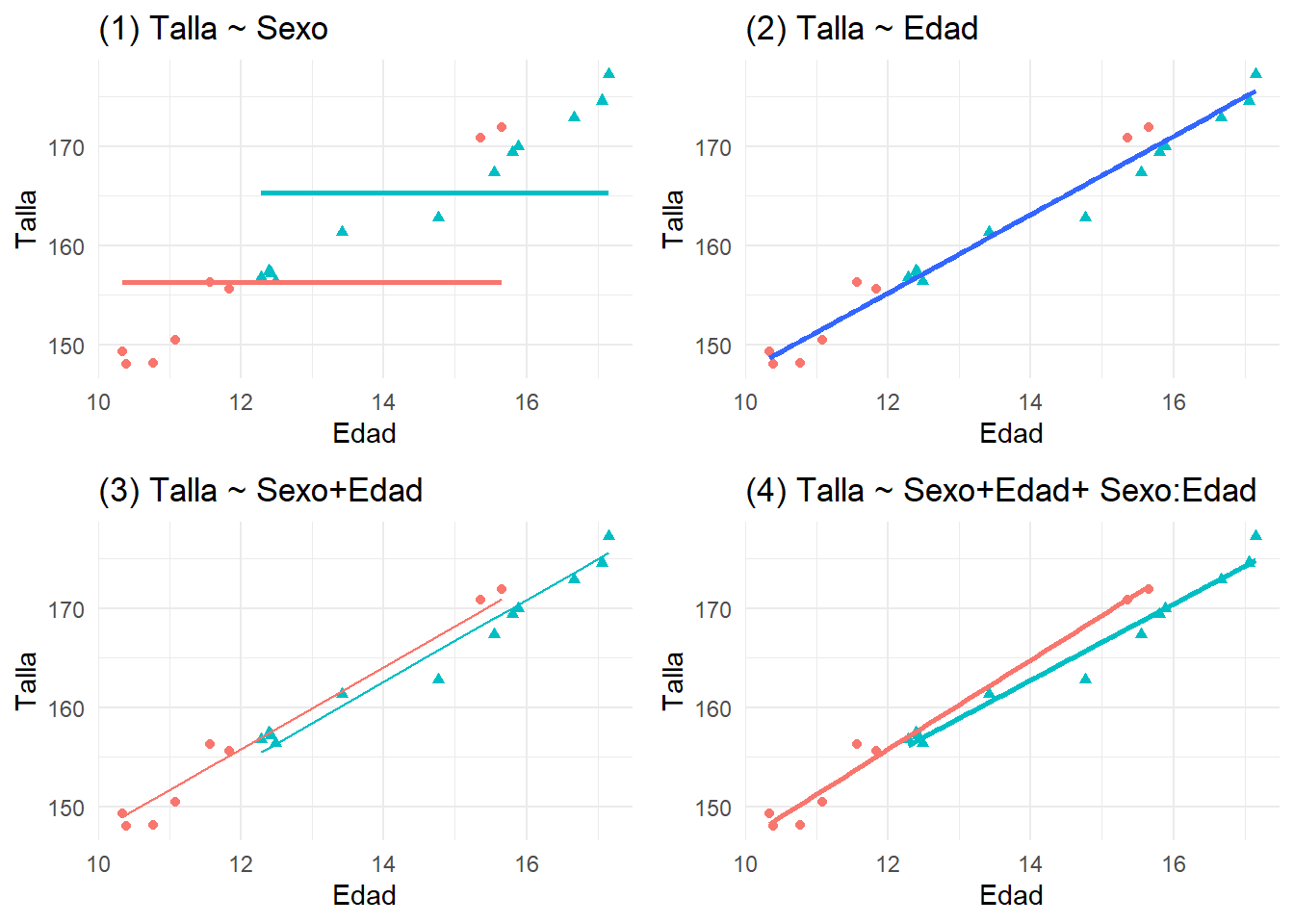

modeloSexo <- df %>% lm(Talla ~ Sexo, data=.)
modeloEdad <- df %>% lm(Talla ~ Edad, data=.)
modeloSexoEdad <- df %>% lm(Talla ~ Sexo+Edad, data=.)
modeloInteraccion <- df %>% lm(Talla ~ Sexo*Edad, data=.)
tab_model(modeloSexo, modeloEdad,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	156.33	3.01	<0.001	107.74	2.21	<0.001
Sexo: Mujer	8.96	3.89	0.033
Edad				3.96	0.16	<0.001
Observations	20			20
R² / R² adjusted	0.227 / 0.185			0.971 / 0.970
AIC	146.374			80.389

tab_model(modeloSexoEdad,modeloInteraccion,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	106.26	2.24	<0.001	101.63	3.05	<0.001
Sexo: Mujer	-1.51	0.84	0.089	7.47	4.45	0.113
Edad	4.13	0.18	<0.001	4.51	0.25	<0.001
SexoMujer:Edad				-0.68	0.33	0.057
Observations	20			20
R² / R² adjusted	0.976 / 0.973			0.981 / 0.977
AIC	78.882			76.218

Ejemplo 6

Descargue la base de datos regresion-200-3.sav. Como el ejemplo anterior, pero usando muestras grandes, donde es más fácil apreciar las interacciones. ¿Que ve que haya cambiado con respecto al ejemplo anterior?

df=read_sav("datos/regresion-200-3.sav", user_na=FALSE) %>% haven::as_factor() %>% 
  mutate(Sexo=Mujer) %>% select(Sexo,Edad,Talla)

dfAumentado <- broom::augment(lm(Talla ~ Edad+Sexo,data=df))
plot_SoloSexo=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE,formula = y ~ 1)+ggtitle("(1) Talla ~ Sexo")+ guides(color=FALSE,shape=FALSE)
plot_SoloEdad=ggplot(df, aes(x=Edad,y=Talla))+geom_point(aes(shape=Sexo,color=Sexo))+
  geom_smooth(method = "lm",se=FALSE)+ggtitle("(2) Talla ~ Edad")+ guides(color=FALSE,shape=FALSE)
plot_SexoEdad=ggplot(dfAumentado, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_line(aes(y = .fitted))+ggtitle("(3) Talla ~ Sexo+Edad")+ guides(color=FALSE,shape=FALSE)
plot_Interaccion=ggplot(df, aes(x=Edad,y=Talla,shape=Sexo,color=Sexo))+geom_point()+
  geom_smooth(method = "lm",se=FALSE) +ggtitle("(4) Talla ~ Sexo+Edad+ Sexo:Edad")+ guides(color=FALSE,shape=FALSE)
grid.arrange(plot_SoloSexo,plot_SoloEdad,plot_SexoEdad,plot_Interaccion)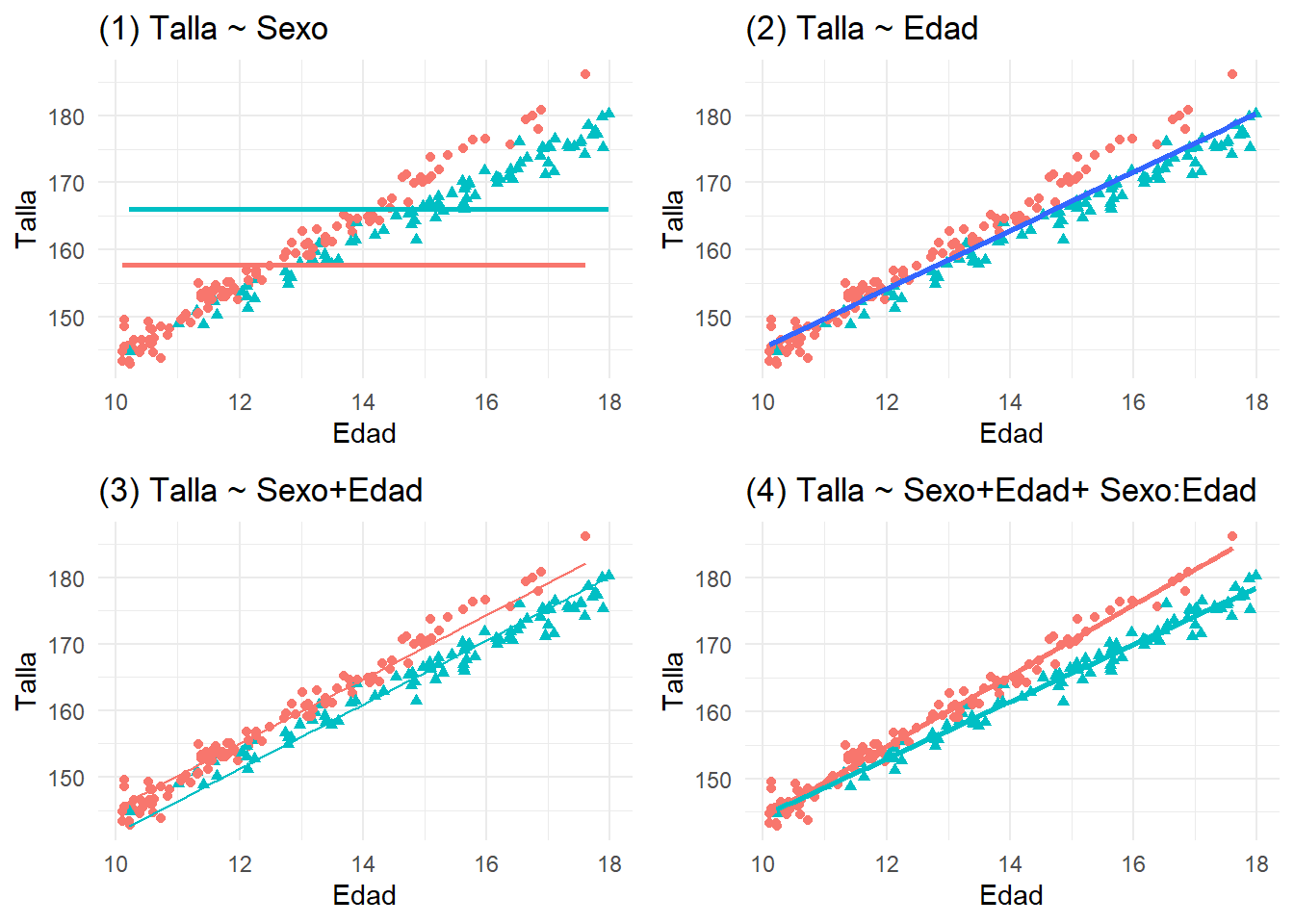

modeloSexo <- df %>% lm(Talla ~ Sexo, data=.)
modeloEdad <- df %>% lm(Talla ~ Edad, data=.)
modeloSexoEdad <- df %>% lm(Talla ~ Sexo+Edad, data=.)
modeloInteraccion <- df %>% lm(Talla ~ Sexo*Edad, data=.)
tab_model(modeloSexo, modeloEdad,show.se = TRUE,show.ci = FALSE,show.aic = TRUE) %>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	157.72	0.90	<0.001	101.57	1.00	<0.001
Sexo: Mujer	8.32	1.35	<0.001
Edad				4.37	0.07	<0.001
Observations	200			200
R² / R² adjusted	0.160 / 0.156			0.949 / 0.948
AIC	1472.594			913.558

tab_model(modeloSexoEdad,modeloInteraccion,show.se = TRUE,show.ci = FALSE,show.aic = TRUE)%>% .[["knitr"]] %>% 
    asis_output()

	Talla			Talla
Predictors	Estimates	std. Error	p	Estimates	std. Error	p
(Intercept)	97.15	0.81	<0.001	91.26	0.90	<0.001
Sexo: Mujer	-3.81	0.29	<0.001	10.46	1.48	<0.001
Edad	4.82	0.06	<0.001	5.29	0.07	<0.001
SexoMujer:Edad				-1.02	0.10	<0.001
Observations	200			200
R² / R² adjusted	0.972 / 0.972			0.981 / 0.981
AIC	792.170			714.491

8 Regresión logística binaria